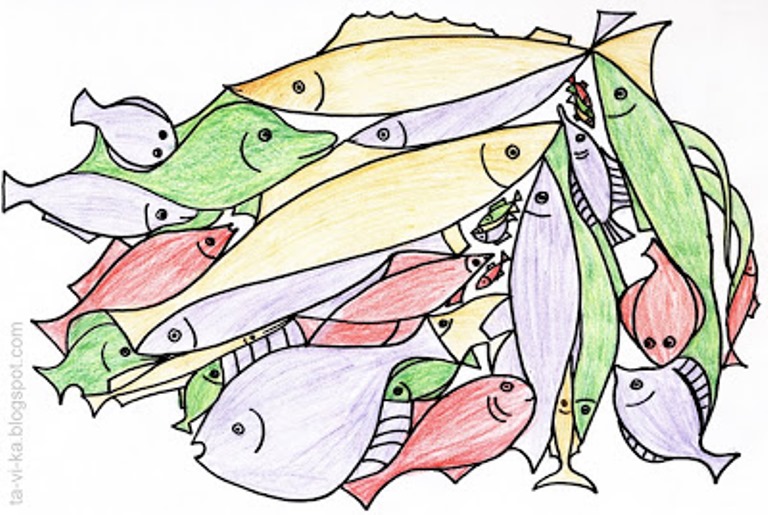
Многие мамы, наверное, догадались, что это детский вариант знаменитой математической теоремы. Так называемой "Проблемы четырех красок". Ее в 1852 году сформулировал Фрэнсис Гутри. Его вопрос звучал так: "Можно ли всякую карту раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета". Практика показывает, что можно. Никто и никогда не мог нарисовать пример карты, опровергающий это утверждение. Но вот строго математически это доказать удалось лишь в 1976 году! Да и то с помощью компьютера. Доказательство теоремы столь сложно, что пока ни один ученый не проверил полностью все выкладки. Поэтому некоторые математики считают, что это доказательство некорректно и не принимают его.
Если ребенку будет интересно, можно даже поиграть в игру "Четыре краски". Участвуют два или четыре игрока. Для нее понадобится лист бумаги и четыре цветных карандаша. Лист бумаги делится на области произвольным образом. Карандаши делятся между игроками (если играет два человека, то берется по два карандаша каждому). После этого игроки по очереди закрашивают по одной области на карте своими карандашами. Главное условие, что граничащие области не должны быть одного цвета. Тот игрок, который не сможет сделать следующий ход, проиграл. Если всегда правильно выбирать варианты раскрашивания, то будет ничья:)